Last night, my 12-year-old son and I were engrossed in solving math puzzles on TED Ed via YouTube, sometimes collaboratively and sometimes competing with each other. My son and I enjoy playing together and competing on things ranging from math and programming to pickleball and wrestling.
It was another of those evenings where learning and bonding intersect. My son wasn’t feeling his best (you know how it goes – kids and their knack for picking up every bug going around), but we discovered that tackling these brain teasers together was a fun and helpful distraction while he recovers.
Our shared enthusiasm for challenging AI language models with tricky math and reasoning problems has become a tradition. Earlier, we wrote about our adventures in prompt engineering to generate code for solving math problems . It is thrilling to pit our wits against these AI “brains”, seeing where they excel and where they stumble.
This time, we took a screenshot of a math puzzle from the TED Ed channel displayed on our TV screen. Armed with this visual puzzle, we set out to challenge three different AI language models: OpenAI’s ChatGPT GPT-4o, Anthropic’s Claude 3.5 Sonnet, and Google’s Gemini Pro 1.5. All of these models have some level of multimodal capabilities, meaning they can process both text and images.
To keep things fair and simple, we gave each AI the same straightforward prompt accompanying the screenshot: “Please solve this.” No hints, no extra context — just the raw puzzle and a request to solve it. What we observed was fascinating, and what we learned from it is what I want to dive into today. (I would have normally said “delve into”, but then people like Paul Graham would erroneously think my son and I didn’t write this blog post . Oh well.)
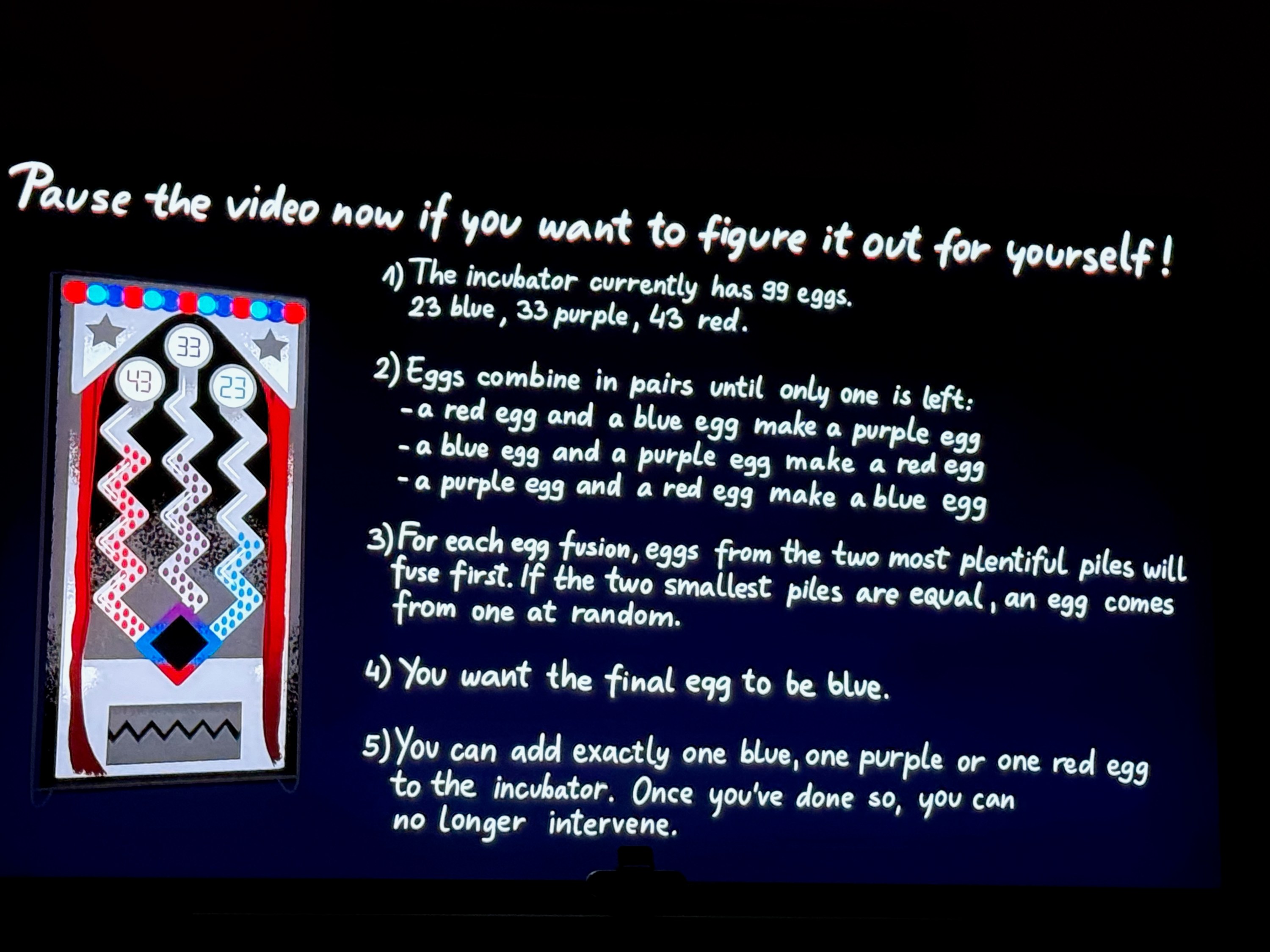
Here is the screenshot summarizing the math puzzle in the video. we’ve embedded the full video at the end of this blog post. You will enjoy this blog post even more if you watch the video.
Here is the text from the screenshot:
Pause the video now if you want to figure it out for yourself!
- The incubator currently has 99 eggs. 23 blue, 33 purple, 43 red.
- Eggs combine in pairs until only one is left:
- a red egg and a blue egg make a purple egg
- a blue egg and a purple egg make a red egg
- a purple egg and a red egg make a blue egg
- For each egg fusion, eggs from the two most plentiful piles will fuse first. If the two smallest piles are equal, an egg comes from one at random.
- You want the final egg to be blue.
- You can add exactly one blue, one purple or one red egg to the incubator. Once you’ve done so, you can no longer intervene.
Below are the three responses we got.
First, Anthropic Claude 3.5 Sonnet, who got it wrong… but don’t take that to mean it isn’t as good as the ones who got it right. Please read our analysis at the end of this post.
Anthropic Claude 3.5 Sonnet ❌
Let’s approach this problem step-by-step:
- Initial state: 23 blue eggs, 33 purple eggs, 43 red eggs (total 99 eggs)
- We need to end up with a blue egg, so we need to work backwards.
- To get a blue egg as the final result, the last fusion must be between a purple egg and a red egg.
- Let’s simulate the fusions:
- Red (43) + Blue (23) -> 23 Purple eggs Now we have: 0 Blue, 56 Purple, 20 Red
- Purple (56) + Red (20) -> 20 Blue eggs Now we have: 20 Blue, 36 Purple, 0 Red
- Blue (20) + Purple (36) -> 20 Red eggs Now we have: 0 Blue, 16 Purple, 20 Red
- Purple (16) + Red (20) -> 16 Blue eggs Now we have: 16 Blue, 0 Purple, 4 Red
- Blue (16) + Red (4) -> 4 Purple eggs Now we have: 12 Blue, 4 Purple, 0 Red
- At this point, we’re left with 12 Blue and 4 Purple eggs. We need one more Purple egg to create the final Blue egg.
- According to rule 5, we can add exactly one egg of any color. We should add one Purple egg.
- After adding one Purple egg: 12 Blue, 5 Purple
- The final fusion: Blue (12) + Purple (5) -> 5 Red eggs Now we have: 7 Blue, 0 Purple, 5 Red Red (5) + Blue (5) -> 5 Purple eggs Now we have: 2 Blue, 5 Purple, 0 Red Purple (5) + Blue (2) -> 2 Red eggs Final result: 0 Blue, 0 Purple, 2 Red Red (2) + Purple (1) -> 1 Blue egg (final egg)
Therefore, to ensure the final egg is blue, we should add one purple egg to the incubator.
Then, Google Gemini 1.5 Pro, who also got it wrong, but with a different incorrect answer. Again, please don’t make assumptions yet, wait for the end of this article…
Google Gemini 1.5 Pro ❌
Here’s how to solve this puzzle:
Understanding the Problem
We have an incubator with three types of eggs that combine in specific ways. We need to ensure the final egg is blue by adding only one egg at the start.
Key Points
- Egg Combinations:
- Red + Blue = Purple
- Blue + Purple = Red
- Purple + Red = Blue
- Fusion Priority: Eggs from the two largest piles combine first.
- Goal: The final egg should be blue.
- Intervention: We can add one egg (blue, purple, or red) only once.
Solution
- Current Situation: We have 23 blue, 33 purple, and 43 red eggs. Red is the largest pile.
- Initial Fusions: Red and purple eggs will combine first, creating blue eggs. This will continue until either red or purple eggs run out.
- Scenario Analysis:
- If red runs out first: We’ll be left with blue and purple eggs. These will combine to form red eggs. We don’t want this.
- If purple runs out first: We’ll have red and blue eggs. These will combine to form purple eggs.
- Desired Outcome: We want the purple eggs scenario. To achieve this, we need to ensure the purple pile is depleted first.
- Intervention: We need to add a red egg. This will increase the red pile, ensuring it lasts longer than the purple pile during the initial fusions.
- Final Steps:
- Add a red egg.
- Red and purple combine to form blue until purple runs out.
- We’re left with red and blue, which combine to form purple.
- Finally, we have red and purple, which combine to form the desired blue egg.
Answer: Add a red egg.
Then, OpenAI ChatGPT GPT-4o, who got the correct answer, and used the correct logical reasoning. It felt like Mr. Spock or Commander Data from Star Trek, not Captain Kirk was solving the problem.
OpenAI ChatGPT GPT-4o ✅
To solve this problem, we need to determine which egg to add (one blue, one purple, or one red) to ensure the final remaining egg is blue. Let’s analyze the situation step-by-step:
Step-by-Step Analysis
- Initial Egg Counts:
- Blue: 23
- Purple: 33
- Red: 43
- Egg Combination Rules:
- Red + Blue → Purple
- Blue + Purple → Red
- Purple + Red → Blue
- Fusion Process:
- Eggs from the two most plentiful piles will fuse first.
- If two piles are equal in size, an egg is chosen randomly from one of them.
- Goal:
- Ensure the final egg is blue.
- Intervention Rule:
- You can add exactly one blue, one purple, or one red egg to the incubator. After adding, you cannot intervene further.
Strategy
To ensure the last egg is blue, consider the parity (odd or even number) of the counts of each color. Each fusion will affect the counts in a particular way, and understanding how these counts change is key.
Parity Analysis
- Blue Eggs: 23 (Odd)
- Purple Eggs: 33 (Odd)
- Red Eggs: 43 (Odd)
When combining eggs according to the rules, each combination will change the number of eggs of two colors. Let’s look at the parity changes:
- Red + Blue → Purple:
- Red decreases by 1.
- Blue decreases by 1.
- Purple increases by 1. This means two odd counts become even, and one odd count remains (or vice versa).
- Blue + Purple → Red:
- Blue decreases by 1.
- Purple decreases by 1.
- Red increases by 1. Again, two odd counts change, and one stays the same.
- Purple + Red → Blue:
- Purple decreases by 1.
- Red decreases by 1.
- Blue increases by 1. Similarly, the change affects two counts.
Each fusion changes two parities, meaning the total parity of the system (number of odd counts) remains the same or changes by 2, always maintaining parity.
Conclusion
To end with a blue egg, we must ensure that the parity of the blue count becomes odd and remains so after all combinations.
Currently, the counts are:
- Blue: 23 (Odd)
- Purple: 33 (Odd)
- Red: 43 (Odd)
Since all are odd, the total count of odd numbers is 3 (odd). To maintain the final egg as blue, we want the final state to have one odd count (blue).
- Adding one blue egg changes the count of blue to 24 (even). Now we have:
- Blue: 24 (Even)
- Purple: 33 (Odd)
- Red: 43 (Odd)
Now, there are 2 odd counts (Purple and Red) and one even (Blue). Any subsequent fusion will always flip the parity twice, thus maintaining the two odds. Eventually, the last remaining egg will be blue if no other intervention is possible.
Solution
Add one blue egg to the incubator to make the final remaining egg blue.
My son and I felt it wasn’t fair that we pitted Anthropic’s mid-tier model (3.5 Sonnet) against Open AI and Google’s top-tier models, so we gave the same problem to Claude 3.0 Opus, who did give us the correct answer, but with a style of probabilistic reasoning, which seems more like guesswork that a human would have done. In this way, even though Anthropic’s Claude models got the wrong answer and an imprecise answer respectively, their responses were the most human-like.
Anthropic Claude 3.0 Opus ☑️❓
Okay, let’s break this down step-by-step based on the instructions in the image:
- The incubator currently has 99 eggs: 23 blue, 33 purple, and 43 red.
- Eggs combine in pairs until only one is left. The combinations are:
- A red egg and a blue egg make a purple egg
- A blue egg and a purple egg make a red egg
- A purple egg and a red egg make a blue egg
- For each egg fusion, eggs from the two most plentiful piles will fuse first. If the two smallest piles are equal, an egg comes from one at random.
- The goal is to have the final egg be blue.
- We can add exactly one blue, one purple or one red egg to the incubator. Once we’ve done so, we can no longer intervene.
So let’s think through the process:
- Currently, the red eggs are most plentiful, followed by purple, then blue.
- Red and purple eggs will fuse first, creating blue eggs until one pile is depleted.
- Then the remaining pile will fuse with blue eggs, creating either red or purple eggs.
- This process continues until one egg remains.
Considering the current counts, adding a blue egg seems most likely to result in a final blue egg. Adding red or purple would make those piles even larger, increasing the chances the final egg is one of those colors instead.
Therefore, I recommend adding one blue egg to maximize the probability that the final egg is blue.
Our Thoughts
The results of our experiment were… what’s the word? Educational. While it’s tempting to declare a “winner” based on which AI got the correct answer, the reality is more nuanced and interesting.
Let’s address the elephant in the room: why did we get such wildly different answers from these sophisticated AI models? There are a few factors at play:
- Training Data Differences: Each AI model is trained on its own unique dataset. It’s possible that OpenAI’s GPT-4o encountered this specific puzzle or similar logic problems more frequently in its training data, giving it an edge in solving this particular problem. Though we’d have thought Google Gemini would be the one most familiar with the content of YouTube videos and their transcripts.
- Reasoning Approaches: The varying responses highlight different approaches to problem-solving. Claude’s step-by-step breakdown, while incorrect, mirrors how a human might tackle the problem. Gemini’s approach shows an attempt at strategic thinking, even if it led to the wrong conclusion. GPT-4o’s parity-based analysis demonstrates a more abstract, mathematical approach.
- Probabilistic Nature: AI responses are probabilistic, not deterministic. Running the same query multiple times might yield different results, especially for complex (for an AI) problems like this one.
This single experiment doesn’t prove the superiority of any models over others. What it does show is the current state of AI problem-solving: impressive, but far from infallible.
The human-like qualities of Claude’s responses, even when incorrect, raise interesting questions about the nature of AI reasoning. Are we more comfortable with AI that “thinks” like us, even if it’s wrong? Or do we prefer correct answers, even if the reasoning feels alien? Remember how Google Deepmind’s Alpha Zero played what some people called “Godlike moves” in Go and Chess?
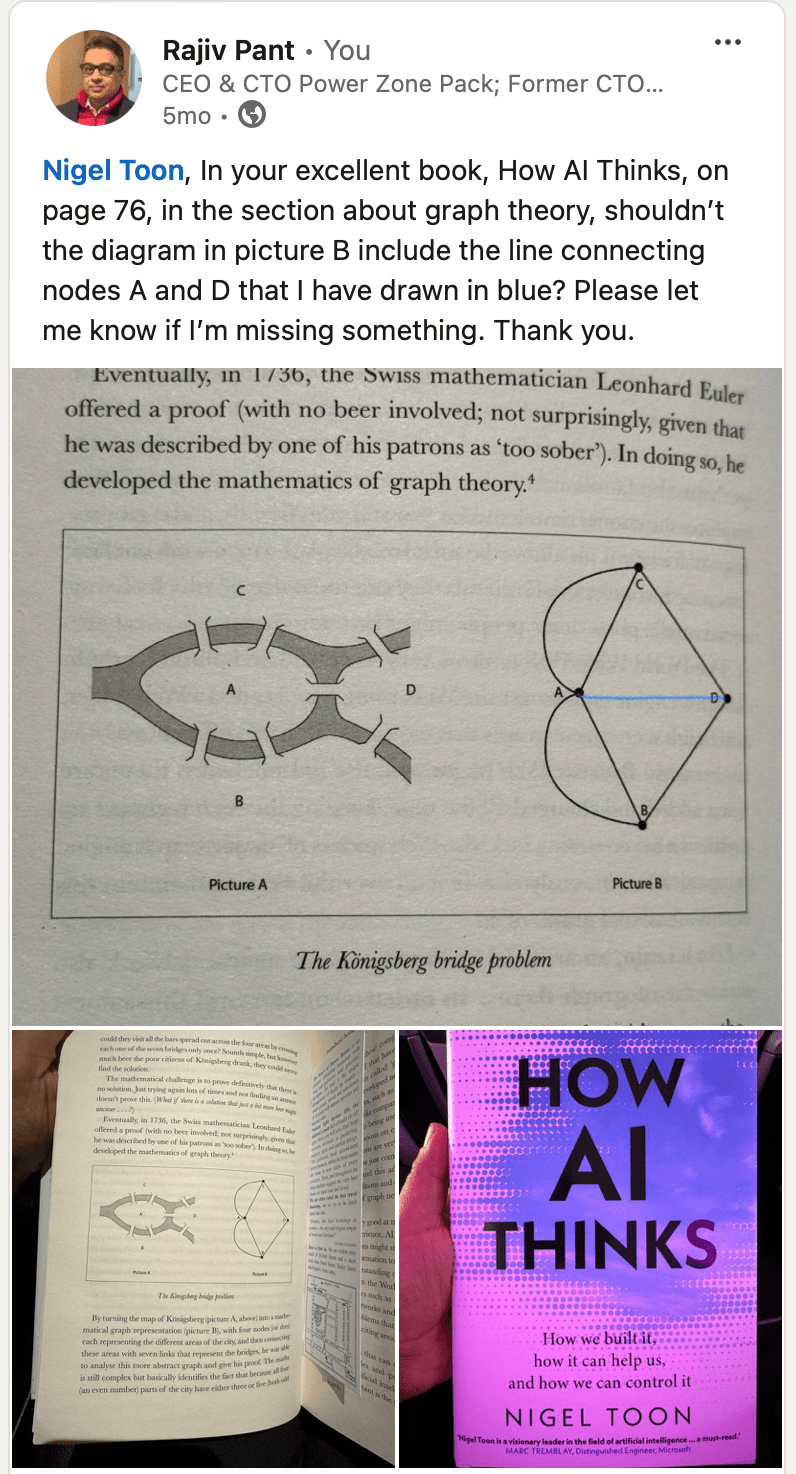
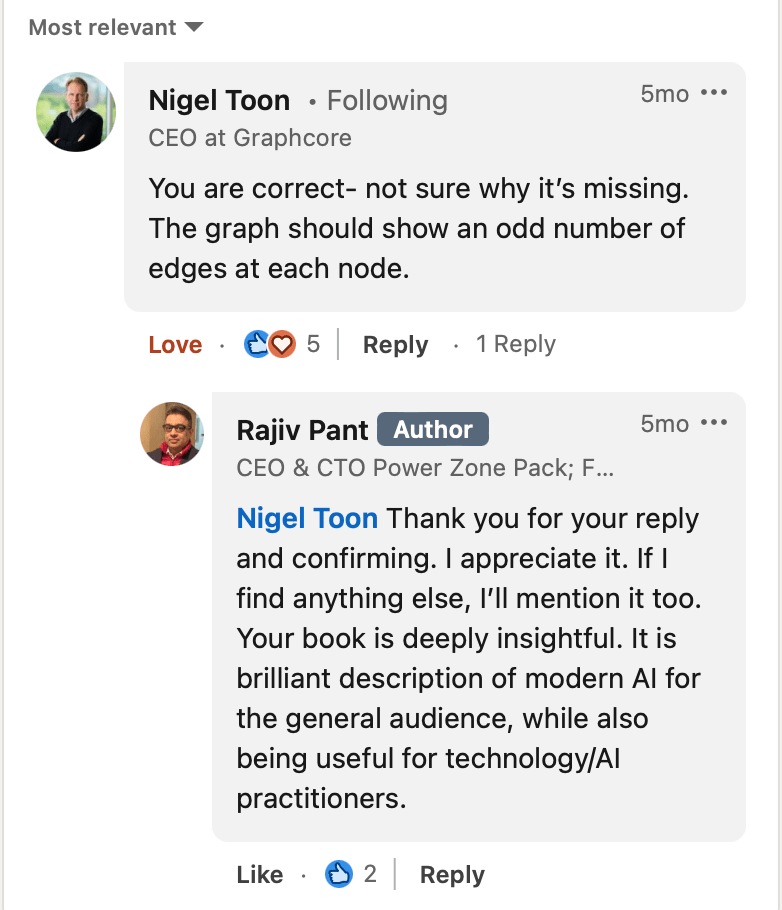
Which reminds me of the excellent book “How AI Thinks” by Nigel Toon. Among other valuable insights, it reminded me that both humans and AI make mistakes.
This experiment also highlights the importance of critical thinking when using AI tools. As powerful as these models are, they’re not omniscient. Their responses should be starting points for further investigation. Remember what happened to that lawyer who used ChatGPT to do his work and got in trouble?
A healthy dose of skepticism is useful as we integrate AI more deeply into our lives.
My son and I enjoy imagining how these models will evolve. Will we see more consistency in problem-solving across different AI platforms? Or will distinct “personalities” and problem-solving styles emerge?
My son and I will keep posing tricky questions to these AIs, pushing their capabilities, and learning from their limitations. Such discovery is both entertaining and enlightening.
The competition for a humans is not AI, but other humans using AI to augment their own capabilities.
The Puzzle Video
Here is the full video of the puzzle:
Update (2025 January 27)
Following the release of OpenAI’s o1 and DeepSeek’s DeepThink R1 reasoning models, I have been experimenting with those models and have published my findings in a follow up blog post titled The Evolution of AI Reasoning: A Follow-up Analysis: OpenAI o1 vs. DeepSeek’s DeepThink R1 .